在教育、科技、工程、人事等管理领域中,评价既是为决策提供依据和支持的工具,同时也是诊断、鉴定、激励和监控的重要手段而得到广泛开展,如教育评价、科技评价、工程项目评价、人员评价……等等①②。现实生活中的评价工作通常是多属性综合评价,即根据评价对象的多个属性与特征,对评价对象作出全局、整体的价值评判,并根据评价对象的总价值大小实现多个评价对象的优劣排序或者将所有的评价对象划分为若干个等级。
本文在分析综合评价中常用数据处理方法的基础上,提出一种基于奖优惩劣思想的综合评价方法,以提高评价对象之间的区分度,并通过实例表明该方法是合理有效的。
一、综合评价中的数据处理由于复杂对象的总价值难以直接衡量和测定,因此综合评价中通常是按照系统科学的方法将评价对象进行自上而下的逐层分解,直到分解为可以直接测定价值的构成要素为止,形成具有层次结构的树状评价指标体系,由此实现对评价对象的价值评判工作转换为对各项末级指标的价值评判工作③。综合评价中的数据处理主要包括各项指标属性值的规范化处理与将各项指标的价值合成为评价对象总价值的处理等。
(一) 指标属性值的规范化处理指标体系中各项指标从不同的方面体现了评价对象的属性与特征,因此各项指标的物理含义、量纲、数量级等各不相同;各项指标的类型也不尽一致,如有的指标是效益性指标(指标属性值越大则对评价对象总价值的贡献也越大),有的是成本型指标(越小越好的指标),而有的是适中型指标(属性值在某个区间范围内最好);指标体系中还往往是主观指标与客观指标并存,主观指标按照人为评判方式不同,其属性值又有百分制形式、等级形式、多评价对象的排列序位形式等多种形式。因此,不同量纲、不同类型的指标属性值是无法直接合成为评价对象的总价值。
指标属性值的规范化处理是把不同量纲、不同类型的指标原始属性值x通过某效用函数f(x),通常转换为[0, 1]区间内没有量纲、类型一致的相对价值,转换结果越大表示该项指标对评价对象总价值的贡献也越大,最后根据各项指标的相对价值合成为评价对象的总价值。
效用函数必须满足保序性④,即如果指标的属性值为x1时对评价对象总价值的贡献要比属性值为x2时的贡献大,则效用函数须满足f(x1)>f(x2)。对于效益型指标而言,常用的效用函数有:
| $ {{f}_{1}}\left( x \right)=\frac{x-\rm{Min}}{\rm{Max-Min}} $ | (1) |
| $ {{f}_{2}}\left( x \right)=\frac{x}{\rm{Max+Min}} $ | (2) |
| $ {{f}_{3}}\left( x \right)=\frac{x}{\rm{Max}} $ | (3) |
其中Max和Min分别表示该项指标在所有评价对象中属性值的最大值和最小值。其中f1(x)将指标属性值中的最大者和最小者分别转换为1和0,其余作线性插值处理;f2(x)则以所有评价对象的中间值为基准,转换结果分布在0.5附近;当Max和Min相差不大时,f3(x)保证了所有评价对象的转换结果均接近于1。
对于成本型指标和适中型指标而言,效用函数实质上是将成本型指标和适中型指标转换为效益型指标。例如成本型指标的效用函数可以是上述效益型指标效用函数的变形:
| $ {{f}_{4}}\left( x \right)=1-{{f}_{i}}\left( x \right)\rm{ }\left( \mathit{i}=1,2,3 \right) $ | (4) |
或者
| $ {{f}_{5}}\left( x \right)=\frac{1}{x} $ | (5) |
显然,效用函数并不唯一,选用不同的效用函数可能会导致不同的转换效果。
(二) 多指标数据的合成综合评价中将多项指标的价值合成为评价对象的总价值是一个逐级合成的过程,即按照指标体系的层次结构,自下而上将若干项同属于一个上级指标、处于同一层次的“兄弟”指标的价值合成为其“父节点”的价值,直到最后合成为评价对象的总价值。
在树状评价指标体系的某一棵“子树”中,如果各项“兄弟”指标属性值的规范化处理结果分别为x1,x2 ,…,xn,各项指标的权重分别为w1,w2 ,…,wn。在权重归一化的情况下(wi≥0且∑wi=1),由各项指标的价值合成为上级指标价值的合成模型通常有加法合成模型和乘法合成模型⑤:
| $ {{f}_{6}}({{x}_{1}},{{w}_{1}},{{x}_{2}},{{w}_{2}},\ldots ,{{x}_{n}},{{w}_{n}})=\sum\limits_{i=1}^{n}{{{x}_{i}}\times {{w}_{i}}} $ | (6) |
| $ {f_{7}}({x_{1}},{w_{1}},{x_{2}},{w_{2}}, \ldots ,{x_{n}},{w_{n}}) = \mathop \prod \limits_{i = 1}^n {\rm{ }}{x_{i}}^{{w_i}} $ | (7) |
加法合成模型是综合评价中最常用的合成模型,其最大特点是补偿性能,即上级指标的价值可由各项下级指标相互补偿,某些指标价值的下降(或上升)可通过其它指标价值的上升(或下降)得到有效补偿。加法合成模型强调主因素的作用,权重较大的下级指标体现了上级指标的主要特征,对上级指标的价值起决定性的作用。乘法合成模型的最大特点是强调各项指标价值的均衡性,一般情况下各项指标的价值不能有效地相互补偿,一旦任何一项指标的价值较小(接近于0),纵使该指标的权重很小,其上级指标的价值也就很小。不同的合成模型具有不同的特点和适用场合,选用不同的合成模型势必导致不同的评价结果。因此,需要结合评价方针、各项指标的特性等选用合适的合成模型。
由于指标的属性值经过规范化处理以后,所有指标的性能均为效益型指标,并且所有指标的价值均在[0, 1]区间内,因此,由各项指标的价值合成而得的评价对象总价值也在[0, 1]范围内,由此根据多个评价对象的总价值大小可以区分各评价对象的优劣程度。
二、基于奖优惩劣思想的综合评价方法指标属性值规范化处理中的[0, 1]区间线性转换法,优点是简单、直观,但也存在明显的缺陷,一是效用函数的性能受到最大值和最小值等个别极端数据的影响,转换结果具有较大的偶然性;二是当各评价对象的属性值分布不均匀时,如次大值远小于最大值或者次小值远大于最小值,则大部分数据的转换结果均集中在[0, 1]区间的低端或高端,降低了分辨率。
为了在指标属性值的规范化处理中更加客观、全面地反映各评价对象在所有评价对象中的相对状况,则可用方差分析法进行指标属性值的规范化处理。对于某项指标而言,所有评价对象的指标属性值分别为x1,x2,…,xn,首先计算标准差S和标准化值Zi(i=1, 2, …, n),再根据标准化值Zi进行数据转换。
| $ S=\sqrt{\frac{1}{n-1}\sum\limits_{i=1}^{n}{{{({{x}_{i}}-\bar{x})}^{2}}}} $ | (8) |
| $ {{Z}_{i}}=\frac{{{x}_{i}}-\bar{x}}{S} $ | (9) |
其中:
| $ \bar{x}=\frac{1}{n}\sum\limits_{i=1}^{n}{{{x}_{i}}} $ | (10) |
标准化值Zi是没有量纲的,与原始数据的量纲及数量级大小均无关。而且,标准化值清晰地体现了原始数据xi在所有数据中的偏离程度,当Zi=0时,表示xi等于所有数据的平均值;当Zi>0时,表示数据xi大于平均值;当Zi < 0时,表示数据xi小于平均值;Zi偏离0越远则表示xi偏离平均值越远。
由于效用函数转换结果的取值范围一般为[0, 1]区间,而根据标准化值Z进行指标属性值x的规范化处理时,为了使转换结果也直观地反映指标属性值x的偏离程度,可以设定平均值的转换结果为0.5,大于平均值的转换结果大于0.5,越大者转换结果越接近于1;反之,小于平均值的转换结果小于0.5,且越小者转换结果越接近于0。显然,Sigmoid函数⑥完全符合效益型指标的规范化处理要求:
| $ f\left( Z \right)=\frac{1}{1+{{e}^{-Z}}} $ | (11) |
相应地,成本型指标的效用函数可选取:
| $ f\left( Z \right)=1-\frac{1}{1+{{e}^{-Z}}}=\frac{1}{1+{{e}^{Z}}} $ | (12) |
评价实践中根据各项指标的相对价值,通过加法模型合成为评价对象的总价值,经常出现评价对象的总价值比较接近的现象。为了提高评价结果的区分度,拉开不同评价对象总价值的差距,在不更改多指标数据合成模型的前提下,一种有效的方法是在指标属性值规范化处理过程中体现“奖优惩劣”的思想。⑦提出将数据转换结果的取值范围调整为(-1, 1)区间,大于平均值的转换结果为正数,小于平均值的转换结果为负数。其实质是对于小于平均值的评价对象在加法合成模型中进行“倒扣分”,其实只体现了“惩”而没有体现“奖”。
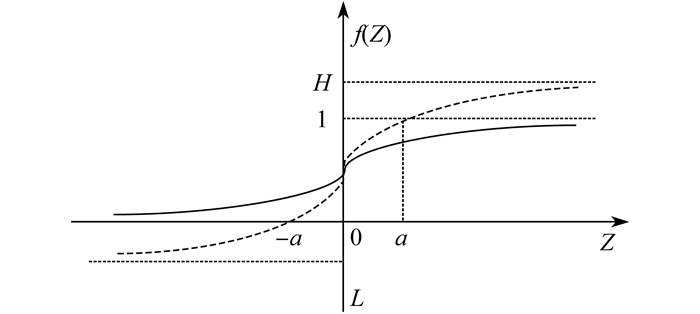
按照“奖优惩劣”的思想,在进行指标属性值转换为相对价值时,将部分表现优异的指标属性值转换为大于1的结果,同时将部分表现不佳的指标属性值转换为小于0的结果,继而在加法合成模型中对表现优异者给予“加分”,对表现不佳者进行“扣分”,以此实现“奖优惩劣”的效果,提高评价结果的区分度。以效益型指标为例,可将Sigmoid函数(如图 1中的实线所示)进行纵向伸展变换,使得当Z>a时f(Z)>1,由Sigmoid函数的对称性可知,当Z < -a时f(Z) < 0,得到图 1中虚线所示的函数图形。变换后函数的取值范围为(L, H),其中L < 0,H>1,并且L=1-H。
|
图 1 Sigmoid函数及其变换 |
将Sigmoid函数进行上述变换,等效于先将Sigmoid函数的图形向上伸展(1-2L)倍,再下移-L个单位,即把Sigmoid函数的取值区间从(0, 1)放大到(0, 1-2L),再调整到(L, 1-L):
| $ f\left( Z \right)=\frac{1}{1+{{e}^{-Z}}}\times \left( 1-2L \right)+L=\frac{1-L+L{{e}^{-Z}}}{1+{{e}^{-Z}}} $ | (13) |
由于f(-a)=0,代入(13)式可得:
| $ L=\frac{1}{1+{{e}^{a}}} $ | (14) |
因此:
| $ f\left( Z \right)=\frac{{{e}^{-Z}}-{{e}^{a}}}{(1+{{e}^{-Z}})(1-{{e}^{a}})} $ | (15) |
采用方差分析法得到指标属性值的标准化值,根据统计学知识,在标准正态分布情况下,标准化值Z在±3个标准差的范围内包含了99.74%的样本数据⑧,其中部分典型Z值下大于Z值(或小于-Z)的数据占比如表 1所示。
| 表 1 典型Z值下的数据占比 |
因此,对于每一项指标而言,如果要对所有评估对象中最优的10%进行“奖”,同时对最差的10%进行“惩”,则可取a=1.28;同理,如果“奖”和“惩”的比例各为20%,则取a=0.84。
三、应用实例以某地高校综合办学实力评价为例说明基于奖优惩劣思想的综合评价方法,选取评价指标体系中的部分核心指标,并将各项指标的权重作归一化处理。选取13所高校的基本数据如表 2所示,其中办学声誉是主观指标,按照“A/B/C/D/E”的等级形式进行社会调查,五个等级分别按相应的隶属度为0.9、0.8、0.7、0.6、0.5进行赋值,并统计调查结果而得。
| 表 2 部分高校的基本数据 |
由于各项指标均为效益性指标,分别按照f1(x)和f3(x)的效用函数,对每一项指标的属性值进行规范化处理,并根据加法合成模型合成为各所高校的综合评价结果,如表 3所示。同时,对每一项指标的属性值按照(9)式计算其标准化值,设定所有高校中进行“奖”和“惩”的比例各为10%,即取a=1.28,根据(15)式的效用函数f(Z)进行规范化处理,并同样按照加法合成模型合成为各所高校的综合评价结果,如表 3所示。
| 表 3 不同效用函数下的评价结果 |
从表 3可以看出,选用不同的效用函数会导致不同的评价结果,甚至个别评价对象的排列序位发生变化,如选用f3(x)效用函数时学校H的评价结果要优于学校L和D。而且,选用不同的效用函数,所有评价对象评价结果的极差(最大值与最小值之差)也不相同,如选用f1(x)效用函数时的极差为0.771,选用f3(x)效用函数时为0.642,选用f(Z)效用函数时为0.938。显然,通过具有“奖惩”功能的效用函数进行数据转换,有效地提高了评价对象的区分度和分辨率,并且保持了评价对象的排列序位基本不发生变化。
四、结语本文针对综合评价中多个评价对象的评价结果相近的情况,构造了一种基于奖优惩劣思想的效用函数,而且予以“奖”和“惩”的比例可通过参数设置动态调整,通过方差分析得到指标属性值的标准化值进行数据转换,物理概念清晰,评价结果合理,并且有效地提高了评价对象的区分度和分辨率。


