2 西南大学数学与统计学院,重庆 400715;
3 重庆市教育考试院,重庆 401147
2 School of Mathematics and Statistics, Southwest University, Chongqing 400715, China;
3 School of Chongqing Educational Examination, 401147, China
高考对试题命题和质量的评价至关重要。目前,试卷的制定和评价主要是基于经典测量理论(Classical Test Theory, CTT)和项目反应理论(Item Response Theory, IRT)。CTT利用桑代克(E.L. Thorndike)“凡物之存在必有其数量”和麦柯尔(W.A.McCall)“凡有数量的东西都可以被测量”作为理论依据①。根据学生的考试分数进行直接评价,也称为真分数理论。CTT理论试卷评价方法简单、运算方便,易于掌握,是我们目前广泛熟悉和应用的测量理论。它对试卷的评价主要是依靠试题的难度、区分度、效度和信度进行。除了难度是一个比例之外,其余三个指标都是依靠相关性概念来对试卷进行评价分析。CTT理论依靠样本,样本不同对同一份试题的评价也就会产生差别。IRT也称潜在特质理论,起源于20世纪三四十年代的心理测量研究。基于一定假设,用一个数学函数去刻画被试在项目上可观察的作答表现(得分)与其不可观察的特质水平(能力)之间的关系,利用这个函数关系,可以对被试在项目上的作答反应进行预测,同时也可以利用被试在项目上的作答反应对被试的能力进行估计。可以说,模型与假设是整个IRT的核心和基础。目前比较常用的数学模型是二参数逻辑斯蒂模型、三参数逻辑斯蒂模型、Rasch模型和等级评分模型②。
IRT已成为一种新的现代心理与教育测量理论,如SAT、PISA等考试,都是基于IRT的应用。我国现在大学英语四、六级考试也开始运用IRT进行等值研究③。王晓华④、沈南山⑤、赵守盈⑥等人分别就IRT在教育考试命题质量、学业测试、标准化考试等方面进行了研究。但是这些研究都还不涉及实际的普通高考。为此,本文以某地区高考数学数据为例,从项目参数、评价方式和试卷估计精度对CTT与IRT进行比较分析,以期能为IRT应用于高考数学考试提供一种探索性模式。
二、考试数据的结果在这次的高考中,数学试卷包含了填空题、选择题、解答题共3个大题,其中填空题包含5个小题,选择题包含10个小题,解答题包含6个小题,共有21个小题。有十多万被试参加了当年的考试,数据处理采用了IRTP软件和EXCEL进行处理,结果如表 1所示。
| 表 1 IRT与CTT项目指标分布图 |
在用IRT分析测验数据时,首先需针对不同的项目选择不同的模型。填空题选用二参数逻辑斯蒂模型,选择题选用三参数逻辑斯蒂模型,并且c参数取为0.25,解答题选用等级评分模型。试题解答是需要设置步骤的,并根据参考答案的给分步骤,也相应设置了节点(得分点),全卷一共有40个节点。在CTT中,对选择题和填空题的项目难度定义为被试在项目上的正确反应比例,解答题的难度定义为被试在项目上的平均分比项目总分,项目难度的取值范围在0~1之间,难度值越大,项目反而越简单,也就是说项目的难易程度与难度指数的大小是反序的。项目区分度则定义为被试在测验中获得的总分与项目分数之间的相关系数,由此得到的区分度也叫内部一致性系数。
(一) CTT下的结果分析在CTT下的难度与区分度参数分布如表 2。从表 2可知,在该次考试中,信度系数为0.84。难度指数小于0.3的试题有3题,位于0.3至0.7之间的试题有10题,大于0.7的试题有8题。区分度指数除了有两个题小于0.3以外,其余的值均大于0.3。因此,从CTT的观点来看,该次考试的难度中等偏易,质量较好。
| 表 2 难度与区分度参数分布表 |
在IRT下的难度与区分度参数的分布如表 3。从表 3看到,项目难度或类别难度参数b在-2以下的有1个,位于-2~2内的项目参数或类别参数有36个,大于2的类别难度或项目难度参数有3个。项目或类别区分度参数a小于0.5的有1个,0.5~2的项目有24个,2以上的项目有15个。
| 表 3 项目难度与区分度参数分布 |
在IRT中,难度参数b的取值范围为一切实数,一般要求b参数位于-2~2之间⑦,b参数过大与过小的项目都不利于对被试的能力参数进行有效估计。在本次考试中,有36个项目或类别b参数位于-2~2之间,因此从IRT角度看,这36个项目(或类别)的b参数是合适的,但是项目21有3个类别b参数都大于200。从IRT角度看,这样的试题是过难的。因为无论是高能力的被试或者是低能力的被试都无法对这样的试题做出正确反应,因此这样的试题不能对被试的能力进行有效的鉴别。另外有一道选择题的难度参数为-9.9,它意味着几乎所有的被试都能对该试题做出正确反应,这样的试题仍然不能对被试的能力进行有效鉴别。在IRT中,a参数在理论上可以取一切正实数,但是为了对试题(类别)参数及被试的能力参数进行有效估计,一般要求a参数位于0.5~2之间⑧,过大或者过小的a参数都会对参数的估计精度带来不利影响。然而在表 3中看到,有一个试题的a参数小于0.5,有15个试题或者类别a参数大于2,因此从IRT角度看,这些试题的a参数是不理想的。特别是第21题有3个类别a参数的估计值大于100。第1题的a参数只有0.18,这样的试题对被试的能力估计几乎没有任何贡献。当然这样的结果可能与这套试题是基于CTT制定有关。
三、CTT与IRT项目参数的比较 (一) CTT与IRT项目难度参数的比较从表 1中可知,当CTT中项目难度值相同时,它所对应的IRT中的难度参数值有些差别不大,如第2题和第4题,这是两个选择题,在各节点的难度参数都为0.89。它各节点所对应的IRI难度参数分别为-1.22和-1.11。有些题目差别就大一些,如20题第2节点和第4个节点,CTT难度参数为0.42,IRT难度参数却分别为-0.02和0.95。这就是说,对于相同的试卷,CTT项目难度参数相同时它在IRT中的难度参数并非一致。
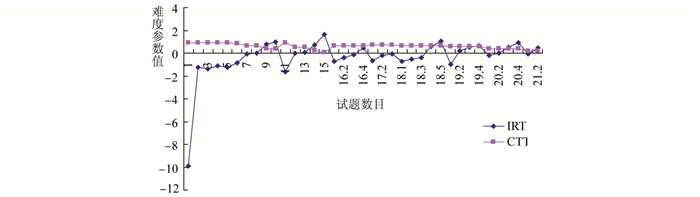
CTT与IRT难度参数比较如图 1所示,横坐标是试题数目, 3表示第3题,16.4表示第16题的第4个节点,纵坐标表示取值。由于IRT里面的21题第3步以后的题目难度区分度值太大,故在对比图里面没有画出。
|
图 1 CTT与IRT难度参数对比图 |
从图 1中可以看出,CTT的难度参数和IRT的难度参数大体相似,但在某些项目上存在差异。可以发现,CTT和IRT的项目难度曲线走势(即高低变化)大致相近,但IRT的变化更加鲜明一些、敏感一些,更容易观测各个项目的特征属性。⑨
(二) CTT与IRT项目区分度参数的比较从表 1可以看出,当CTT中项目区分度参数值相同时,它所对应的IRT中项目区分度参数值差别不大,如第2题和第3题。这是两个选择题,在CTT下的区分度参数都为0.52,在IRT下的区分度参数分别为1.30和1.48。有些题目差别就大一些,如第20题第3、4节点,CTT区分度参数为0.75,IRT却分别为2.71和3.55。在CTT下区分度参数值为0.75,这是一个尚可的值,在IRT下的值为2.71和3.55,却是一个较差的值。这就说,对于相同的试卷,CTT项目区分度参数相同时它在IRT中的区分度参数并非一致。
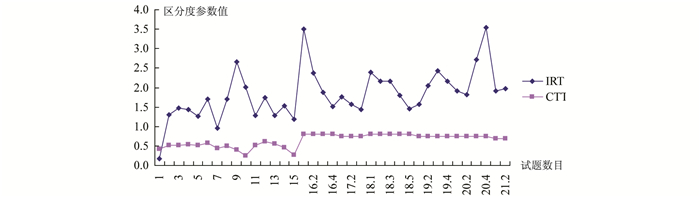
CTT与IRT区分度参数的比较如图 2所示。从图 2可以看出,区分度参数具有难度参数同样的特征,IRT区分度参数更容易观测各个项目的特征属性。
|
图 2 CTT与IRT区分度参数对比图 |
当CTT中区分度与难度参数一致时,它所对应的IRT中区分度与难度参数值差别不大,如第3题和第11题,在CTT中区分度与难度参数值一致,分别为0.52和0.92,在IRT中所对应的区分度与难度参数却是不同的,第3题区分度和难度参数分别为1.48和-1.38,第11题区分度与难度参数分别为1.28和-1.64。有些题差别就大一些,如20题第2和第3节点,在CTT中区分度与难度参数为0.75和0.42,在IRT中区分度与难度参数却分别为1.82、-0.02和2.71、0.50。
综上可知,CTT参数在反映试题的难度和区分能力上有些粗糙,IRT参数比CTT参数更精确的反映试题参数问题。
(四) 项目信息函数在CTT中对试题的评价主要是基于难度和区分度。IRT的试题评价不仅仅是难度和区分度这两个指标,重要的是引入项目信息函数这个概念。例如第11题的项目信息函数图如图 3。
|
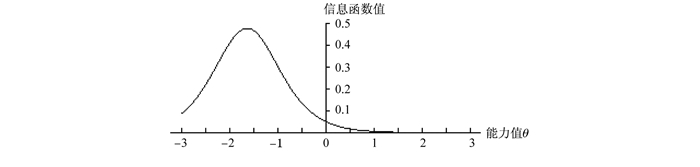
图 3 第11题项目信息函数 |
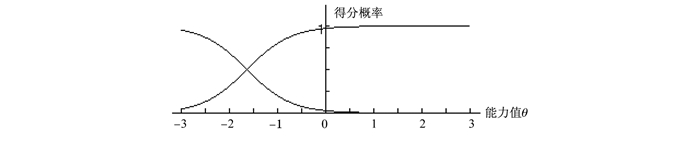
从图 3可知,第11题的项目信息函数值在0.5附近,它所提供的信息一般。在θ=-1.6时,达到峰值,对于能力-1.6的被试提供了最大的信息。在能力大于和小于的被试提供了较少的信息,这个题目适合低水平能力的被试。它的IRT难度与区分度参数分别为-1.64和1.28,项目特征曲线如图 4,也是被试得0分和1分的概率图。IRT对题目的评价主要是看该试题与这个能力段的被试是否匹配。在CTT下第11题的难度是0.92,区分度是0.52。它的难度不好,但区分度较好。再比如,第12题的项目信息函数如图 5。
|
图 4 第11题项目特征曲线 |
|
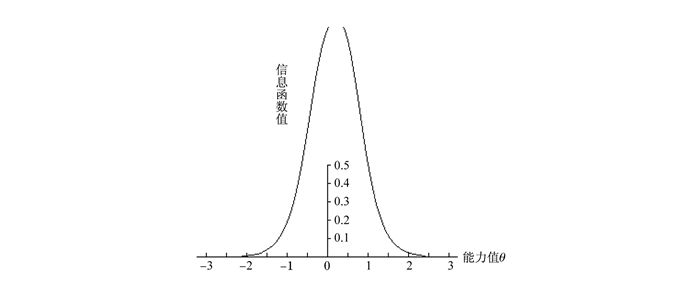
图 5 第12题项目信息函数 |
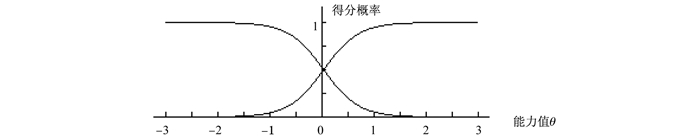
从图 5可知,第12题的项目信息函数值远远大于0.5,它提供的项目信息很好。在(-0.5, 0.5)提供了较多的信息,对在这个能力区间的被试提供了较大的信息,尤其对于能力0.2附近的被试提供了最大的信息量,对于能力大于1.5和能力小于-1.5的被试提供的信息较差。它的IRT区分度与难度参数分别为1.75和0.03,项目特征曲线如图 6。CTT难度与区分度参数分别为0.54和0.62,说明CTT下试题区分度较好。从上可知,CTT是绝对的,IRT对试题进行评价更精细、更客观,而且是相对的。
|
图 6 第12题项目特征曲线 |
在CTT中以学生的测验分数代替学生的能力,所有被试的数学成绩分布如图 7所示。
|
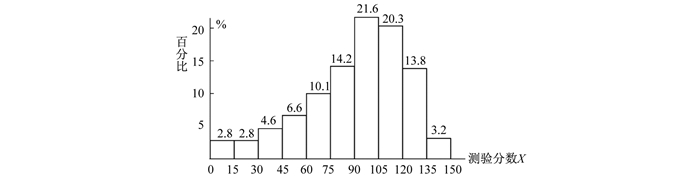
图 7 测验分数分布 |
从图 7可知,被试的测验分数分布呈现明显偏态分布,其峰值位于90分至105分之间,高分数段的被试所占比例较多,低分数段被试所占比较小。这说明当年高考数学试题偏易,这与难度指数的分布情况是一致的。
在IRT中主要用能力参数描述被试的学业成就,由于人们对能力参数不习惯,为此可以将能力参数转换为人们熟悉的“分数”。设
| $ X = \left\{ {\begin{array}{*{20}{c}} {0, \;\;\theta \le-2.5}\\ {30\left( {\theta + 2.5} \right), \;-2.5 < \theta }\\ {150, \;\theta \ge 2.5} \end{array}} \right.\;\;\;\; < 2.5 $ |
通过上述转换,X的取值范围为0~150,与测验分数的取值范围一致。由于X是由能力参数转换得到的,因此我们称X为能力分数。能力分数估计量是相合估计。就是说,如果某一被试的能力分数真值为X0,
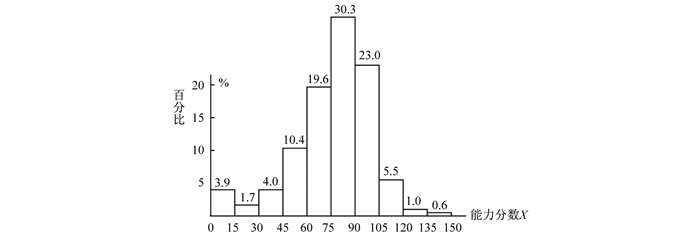
所有被试的数学能力分数分布如图 8所示。从图 8可以看出,被试的能力分数分布与测验分数分布存在较大差异,能力分数分布呈现明显的正态分布特征,其峰指出现在75~90分之间,占被试总数的30.3%。能力分数位于105~120分与120~135分之间的被试分别占总数的5.5%和1%,测验分数占比分别为20.3%和13.8%的比例均有较大幅度降低。位于135~150分之间的被试也由3.2%降低到0.6%。这表明在IRT框架下,去掉了一些虚假的高分,使分数的分布更趋于合理。
|
图 8 能力分数分布 |
在CTT中,对测验精度主要用信度和测验标准误来进行刻画。该次数学考试的信度系数为0.84,测验的标准误12.52,学生测验分数与真实分数之间的平均误差是12.52。信度是一个笼统的、粗略的指标,它只是大致的描述了被试的测验分数与真实分数之间的平均误差。
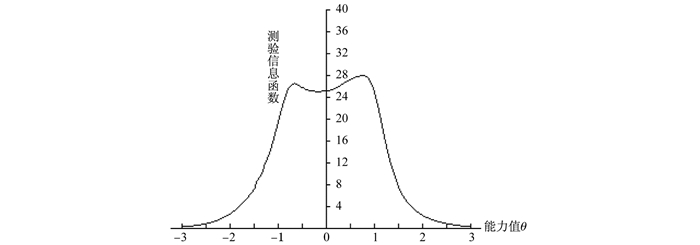
在IRT中,刻画试卷信度是利用测验信息函数这个概念,整体评价。试卷的测验信息函数如图 9所示。
|
图 9 测验信息函数 |
从图 9中可以看出, 在区间(-1, 1)内,测验信息函数值均大于25,该测验提供了较大的信息量,而在这之外则提供了较少的信息量,说明这是一次不错的测验。从图 9可以看出,该图呈双峰型,在能力值-0.8和0.9附近,该项目的信息量分别达到了两个不同的峰值。而在(-0.5, 0.4)之间存在一个凹区间,因此在这个区间提供的信息量较少。
在IRT中,刻画测验误差的方法则是置信区间,IRT能力分数估计95%的置信区间为
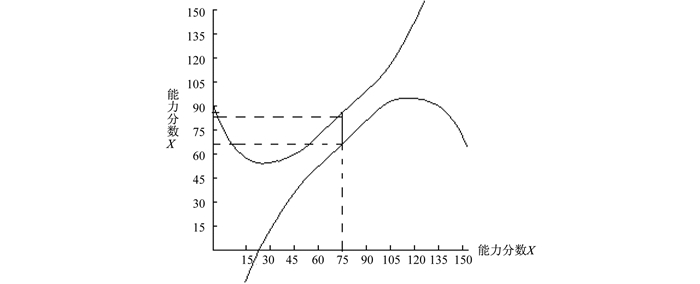
该次测验能力分数估计值95%的置信区间如图 10所示,其中,横坐标为能力分数的估计值,纵坐标表示能力分数真值,下曲线表示置信区间的左端点曲线,上曲线表示置信区间的右端点曲线。比如假设某被试的能力分数估计值为75分,那么在95%的意义下,该被试的真实分数约位于64~85分之间。
|
图 10 能力分数置信区间 |
从图 10看到,在该次考试中,对能力分数位于45~105分的被试的估计精度较高,其估计误差略为11分左右,而对能力分数估计值位于45~105分以外的被试,其估计误差较大。特别是对能力分数估计值大于130和小于30分的被试,其估计误差大于30分,这样大的估计误差实际上已经没有多大的意义。这一结果说明,在同一次测验中,对于不同能力的被试,其能力分数的估计误差也不相同。
六、讨论通过上面的数据分析看到,IRT克服了CTT中的许多缺点,主要表现在以下4个方面:
1.在IRT框架下,它的项目参数比CTT框架下的参数值更具有精确性。
2.能力分数分布优于测验分数分布。这表明在IRT框架下,去掉了一些虚假的高分,使分数的分布更趋于合理。
3.IRT比CTT有更好的估计精度。IRT定义了CTT中没有的项目信息函数和测验信息函数,它是一个具体地、动态地刻画项目和测验性能的综合指标。它指出了每个项目在不同能力水平处提供的信息量的大小,IRT抛开了平行形式的信度观念,直接面向测量标准误,用信息函数来计算估计精度。
4.IRT提出试题编制信息量最大原则。IRT提出了测验编制的指导原则,以项目难度与考生能力水平匹配的原则,即信息量最大原则,在实际编制测验时以信息量为指导的原则。
然而,也不能忽视IRT存在的一些不足。目前,在IRT下能力是基于单维性假设。实际上,被试的能力不止一种,IRT也从单维研究走向多维⑪,多维能力参数估计还处于研究之中。应用也需要一定的软件支撑。对项目研究也有一些偏差,个别项目上CTT参数较好,IRT参数值却比较差,这些都还需要继续研究。
总之,虽然IRT目前存在着一些缺陷,但是在教育考试中尤其是高考数学考试中使用IRT进行测验的编制、报告被试的能力水平和项目性能的解释在理论上比CTT更严格、更完备,在实践中也更有效、更公平。


