2 南京财经大学财政与税务学院/公共财政研究中心, 南京 210023
2 School of Public Administration, NanjingUniversity of Finance and Economics, Nanjing 210023, China
21世纪以来,伴随着经济水平和综合国力的持续提升,我国教育财政投入规模日趋扩大。作为政府教育财政投入规模的量化指标,公共教育支出占国内生产总值 (GDP) 和财政支出的比例常常被用作判断教育经费充足与否的评价标准。2010年7月29日,中共中央、国务院印发了《国家中长期教育改革和发展规划纲要 (2010-2020年)》,《纲要》中指出:教育投入是公共财政的重要职能,各级政府要优化财政支出结构,大幅度提高教育财政投入,努力实现财政性教育经费占国内生产总值比例在2012年达到4%的投入目标。①
(一) 当前我国教育财政投入的概况随着我国公共财政管理体制的建立和完善,政府部门在调整财政收入分配的同时,以“公共需求”为导向,将教育服务全面纳入公共财政保障范围,财政性教育经费在此阶段取得了前所未有的增长。2000年,我国财政性教育经费为2562.61亿元,占当年GDP比重仅为2.58%,远低于同期国际平均水平。2012年,我国财政性教育经费总额大幅攀升至22236.23亿元,占当年GDP的4.28%、财政支出的17.69%,首次达到并超过教育财政投入4%的战略目标。据统计,2014年我国财政性教育经费总额跃升至峰值26420.58亿元,与2000年相比,15年间总体规模提高了10倍以上。
目前,我国经济正在向形态更高级、分工更复杂、结构更合理的阶段演化,经济运行处于深度调整期及矛盾消化期,经济发展步入“新常态”。因此,可以预见经济“新常态”下各级政府财政收支压力将越来越大,以往自上而下“运动式”的资源调动改革模式已很难再复制,财政性教育经费增量在后“4%”阶段存在着较大的不确定性。2012年以来,伴随着教育财政投入4%“政策红利”的释放,教育财政投入随即出现增速放缓的迹象。2014年我国财政性教育经费同比增长7.89%,远低于2012年19.64%的增长速度,占GDP比重更是由2012年的4.28%跌至4.15%,教育财政投入4%的“政策红利”已开始逐步消失。
(二) 后4%时代面临的首要问题2013年1月,原教育部部长袁贵仁 (2013)在全国教育工作会议上提出这一问题:财政性教育经费占GDP比例达到4%以后,怎样建立健全教育财政投入增长的长效机制,在巩固已有成果的基础之上不断增加教育财政投入和社会投入?2014年8月,中共中央总书记习近平在中央财经领导小组第七次会议上,要求各级部门研究实施创新驱动发展战略,加快研究创新驱动发展顶层制度设计,通过各项制度政策的修订和完善,形成新增长的动力源泉。2016年2月,教育部公布了《教育部2016年工作要点》,其中第三部分第7条明确要求:督促各地依法落实教育经费法定增长,建立健全教育投入长效机制。
教育财政投入长效机制的首要目标是为教育事业提供充足的资源。政府部门通过统筹教育经费,努力达到或接近与教育系统总体目标产出相匹配的教育财政投入水平 (Baker, 2005)。《国家中长期教育改革与发展规划纲要 (2010-2020年)》中指出:各地政府要根据地方教育发展基本需要和国家办学条件基本要求,制定并逐步提高教育财政拨款基本标准,切实保障不同地区在各自经济社会条件下达到标准所需要的教育财政经费。因此,后4%时代面临的首要问题是:当前我国教育财政充足水平究竟如何?能否满足全国教育事业发展对财政性教育经费的基本需求?教育财政充足水平能否随着财政性教育经费的增加保持稳步提高的趋势?
二、 教育财政投入充足性研究综述教育财政充足水平作为衡量政府教育财政投入的标准之一,不仅可以对教育财政投入增长机制进行综合判断,也可以为将来的制度设计和部门预算提供具有一定参考价值的量化标准。长久以来,国内外学者在考虑教育财政充足性要求的基础之上,对教育经费标准化测算进行了较为广泛的研究和探索。
(一) 国外教育财政投入充足问题研究20世纪90年代,随着美国教育财政投入改革的兴起和发展,教育财政投入的研究焦点逐步由传统的“公平”问题转向对“充足”问题的研究,并逐步总结出成本函数法、成功学区法、实物消耗定额法和专家判断法四种测算教育经费标准值的研究方法。
成本函数法是在控制住学生特征等产出指标的情况下,运用教育生产和成本函数构建模型,通过线性回归方法拟合出单位教育经费支出的边际产出系数,最后以此估算出达到一定水平的教育产出所需要的教育经费规模 (Picus & Blair, 2004);成功学区法选取若干基本达到学业标准的学区作为示范单位,采用组成因素成本核算法抽取满足该示范学区所需要投入的不同要素,再分别计算这些要素的成本,从而测算出满足充足水平的教育经费标准值;实物消耗定额法首先要设定教育规模和办学条件,其次要确定政府部门完成教育教学活动和保障教育事业稳定发展所需要的资源,并乘以对应的价格,计算出相应的成本,最后将各项成本进行加总计算出满足充足水平的教育经费标准值;专家判断法就是把相关教育专家集合在一起,结合他们的专业判断和认知为原型学校 (Prototypical Schools) 设计教育发展策略,最终商定出能够保证学校学生完成预期学业标准所需的资源数量。
(二) 国内教育财政投入充足问题研究长期以来,国内学者对教育财政充足水平的研究往往是以财政性教育经费占财政支出或国内生产总值的预定比例与实际比例之间的差值作为主要的评价依据,由于主客观因素和国内外形势的变化,该预测难以符合实际,未能准确反映出不同时期教育事业发展对教育经费的真实需求。近年来,我国学者通过分解教育经费结构等方法设定充足度指标,形成了一系列极具参考价值的理论成果。
在外部影响因素分解方面,费宇和李晓鹏 (2006)将地区人口规模、教育经费财政负担率、平均受教育年限和地区发展成本差异指数等指标纳入地方教育财政充足度分析框架,对教育财政充足水平进行评价和判断。张新文和李文军 (2013)将教育财政投入过程中的地方任务进行总量分解,把地方政府教育经费支出占GDP的比例设定为判断地方教育经费充足度的量化标准。在教育经费结构内部因素分解方面,倪俊 (2006)从教育经费支出内部结构的研究视角入手,将教育事业费支出结构中人员经费与公用经费之比 (P/N) 设定为考察地区间及区域内教育财政充足度的衡量指标,比较了2003年我国31个省市的教育财政投入充足情况。陈晓宇 (2012)同样从教育过程内部结构入手,运用教育经费结构指标,分析和推断了教育财政投入的充足程度。卜紫洲、侯一麟和王有强 (2011)基于在教育经费数据搜集方面的重要突破,根据20世纪90年代国家教育部门在“普及义务教育评估”验收时,对教育发展和教育经费的量化指标和《义务教育课程设置实验方案》中对教育投入的目标要求,建立县级教育财政投入标准测算模型,计算出2000-2006年我国县级教育财政充足度的分布特征。
国内外学者对教育财政投入充足水平的研究设计,为教育经费标准化测算提供了宝贵的理论支持,但是上述研究方法在具体应用过程中存在着诸多操作性问题。例如:成本函数法需要统一的产出标准值作为分析指标,对统计数据的要求相对较高,较为复杂的统计分析也隐藏了较多的模型假设;成功学区法方面,由于符合成功标准的学区非常少,而且成功学区的特征要素与其他学区不一定相符,因此,也有一定的限度;卜紫洲等学者设置的相关指标缺乏连贯性,仅仅使用一期的教育发展目标值来综合评价连续若干年的教育财政充足水平,在理论层面上缺乏一定的说服力。综上所述,本文基于上述学者的研究成果,通过充足指数的科学设计,拟对21世纪以来我国教育财政投入充足水平进行标准化测算。
三、 教育财政投入充足指数设计美国教育学家Clune W.H.(1995) 指出:教育财政充足是指政府财政部门应该为公共教育发展提供足够的经费支持,促使每一个学生或整个教育事业能够达到特定的教育目标,如:各阶段学生入学率指标等。因此,在研究过程中本文结合我国不同时期《教育事业发展五年规划》中设定的教育事业发展目标,运用Evidence-based和成本函数等计量方法②,设计出我国历年教育财政充足度指数值Adext,继而通过与全国教育财政投入实际值进行比较,得出相应的教育财政充足度指数,具体包括以下三个步骤:
(一) 选取判定教育财政投入充足水平的指标教育财政充足度是一种事后的概念,充足与否的判断取决于教育财政投入后的教育发展结果是否能够达到事先所设定的目标值 (黄斌,钟宇平,2008)。21世纪以来,中国教育部门于2001年、2005年和2012年相继颁布了第十个、第十一个和第十二个《教育事业发展五年规划》。《教育事业发展五年规划》在总结前一阶段教育发展和改革成果的同时,对下一个五年中教育事业发展的战略目标也进行了详细部署,在设定教育发展目标时,通常以各阶段教育入学率作为考评依据。
因此,本文通过对我国历个《教育事业发展五年规划》中教育发展目标的整理,尝试选取各阶段设定的入学率指标,作为Evidence-based方法测算的数据样本。与其他评价标准相比,该指标以政府部门设定的“十五”“十一五”和“十二五”期间教育发展目标为基数,估算结果可以作为判断教育财政投入充足与否的参考标准之一。与此同时,Odden A.R和Picus L.O (2003)指出:Evidence-based方法根据政府教育发展的具体要求确定资源的需求量,测算出来的充足度指数更加规范和直观,公允度相对较高。
(二) 分解满足教育财政投入充足要求的指标通过对我国不同阶段教育发展规划目标的逐年分解,可以得到学前教育入学率等指标的标准值,继而根据各阶段教育发展目标的标准值逆向推算所需要的财政性教育经费,并以此作为判断教育财政投入是否充足的量化标准。现设定t年财政性教育经费标准值为EFts,当年的学前教育、小学、初中、高中和高等教育入学率标准值分别为PERts、EERts、MERts、SERts和HERts,根据它们的相关关系可以构建函数方程如下:
| $ E{F_{ts}} = f\left({PE{R_{ts}}, EE{R_{ts}}, ME{R_{ts}}, SE{R_{ts}}, HE{R_{ts}}} \right) $ | (1) |
通过上述函数方程,可以测算出我国满足充足水平的财政性教育经费标准值。在具体计算过程中,应把《教育事业发展五年规划》颁布前一年的各项指标值作为基数,然后将该阶段《教育事业发展五年规划》中设定的目标值与之比较,把差额均匀地分解到五年之中,从而计算出各年的财政性教育经费标准值。现将我国历次制定的《教育事业发展五年规划》目标值分解,指标分解结果如表 1所示:
| 表 1 全国教育事业发展目标值分解表 % |
在对我国教育事业发展规划目标值进行分解之后,可以根据函数方程 (1) 测算出历年满足充足性要求的财政性教育经费标准值EFts,继而将其与我国历年财政性教育经费实际值进行比较,从而计算出教育财政充足度指数。现设定教育财政充足度指数为Adext,建立函数方程式如下:
| $ Ade{x_t} = \frac{{E{F_{tr}}}}{{E{F_{ts}}}}\frac{{E{F_{tr}}}}{{f(PE{R_{ts}}, EE{R_{ts}}, ME{R_{ts}}, SE{R_{ts}}, HE{R_{ts}})}}\;Ade{x_t} \in \left({0, + \infty } \right) $ | (2) |
其中,EFtr表示全国财政性教育经费在t年时的实际支出值,Adext表示我国t年时的教育财政充足度,其取值在0到正无穷之间。作为一种事后的评价指标,当Adext接近0时,表示政府部门教育财政投入不足,财政性教育经费不能满足教育发展的需求;当Adext等于1时,表示政府部门教育财政投入相对充足,财政性教育经费能够基本满足教育发展的需求;当Adext大于1趋向正无穷大时 (常出现在政府部门突击完成教育事业发展规划阶段性目标的最终报告期年份中),表示政府部门教育财政投入出现过剩,财政性教育经费不仅能够满足教育发展的需求,还可能出现了一定的盈余。
四、 财政性教育经费标准化测算基于对教育财政投入充足指数的设计,本文拟采用成本函数方法测算满足教育事业发展规划的财政性教育经费标准值。在教育财政投入产出变量的选择方面,地方政府在预算支出绩效管理过程中,常常将学龄教育入学率作为评定其产出的重要指标 (孙克竞,2011)。崔玉平 (2010)、钟华 (2011)、贝努瓦·米洛特 (2013)在分析高等教育财政投入的产出效率时,采用了高等教育入学率作为产出指标。因此,基于教育事业发展规划数据指标的可得性和教育经费标准值拟合标准的统一性,本文采用各阶段教育入学率作为教育财政投入产出的量化指标。
(一) 经费标准化测算模型的构建根据成本函数法,首先要拟合出满足我国教育财政投入充足水平要求的标准方程,继而对各项选定的特征指标 (如学前教育入学率PERts等产出指标) 的目标分解值进行回归,从而估算出我国满足教育事业发展规划所需要的财政性教育经费的标准值。综上所述,在函数方程 (1) 基础之上设定成本函数具体形式如下:
| $ E{F_t} = \alpha + {\beta _1}PE{R_t} + {\beta _2}EE{R_t} + {\beta _3}ME{R_t} + {\beta _4}SE{R_t} + {\beta _5}HE{R_t} + {\mu _t} $ | (3) |
其中,EFt为被解释变量,表示第t年财政性教育经费总量;PERt、EERt、MERt、SERt和HERt为被选定的解释变量,依次表示第t年学前教育、小学、初中、高中和高等教育入学率。此外,下标t代表不同的统计年份;α为不可观测的、不随时间而变的因素;μt为随机误差项;βi为各解释变量的待估系数,即单位财政性教育经费的边际产出系数。
为了确保成本函数中边际产出系数估计结果的准确性,本模型采用我国分税制改革以来 (1992-2014年) 共计23年的全国数据作为分析样本,进而运用Stata统计软件对函数方程 (3) 进行计量回归。其中,全国小学、初中、高中和高等教育入学率等数据整理自历年《中国教育统计年鉴》;而全国学前教育入学率数据则根据历年《中国人口和就业统计年鉴》中3-6岁适龄儿童人数与学前教育在校生人数计算得出 (为了与国家公布的数据保持一致,采用3-6岁),计算结果与国家公布的部分年份数据基本一致。运用Stata11.0软件,对财政性教育经费和学前教育入学率等选定指标进行多元线性回归,结果如表 2所示。
| 表 2 教育成本函数回归结果 |
由表 2中可以看到,各阶段教育入学率均为百分数,导致自变量的边际产出系数较大,其中学前教育、小学和初中入学率在5%水平下统计显著,高中入学率在10%水平下统计显著,高校入学率未通过显著性检验。此外,该成本函数的拟合优度R2为0.9811,拟合效果较好,其具体形式整理如下:
| $ \begin{array}{l} E{F_t} = 406394.7 + 61844.61{\rm{ }}PE{R_t} - 411834.7{\rm{ }}EE{R_t} - \\ 27144.89{\rm{ }}ME{R_t} + 9195.27{\rm{ }}SE{R_t} + 15184.23{\rm{ }}HE{R_t} \end{array} $ | (4) |
然而,尽管常规方法回归结果的拟合优度R2和F值令人较为满意,但是拟合出来的教育成本函数与现实情况有较大出入。从教育财政投入与产出的关系上看,财政性教育经费应与各阶段教育入学率水平保持正向相关关系,而回归结果中小学入学率EERt和初中入学率MERt的系数均为负值,即使刨除掉人口波动因素的影响,其回归系数也与常理大相径庭。因此,需对原模型进行进一步的检验。原模型中五个自变量的方差膨胀因子 (VIF) 的平均值为26.05,远远大于经验值10;另一方面,通过对学前教育入学率PERt等自变量之间相关系数的估算,各自变量相互之间的相关系数非常高。综合上述检验结果可以得出结论:原模型存在非常严重的多重共线性,经费标准化测算模型需要进一步修正。
(二) 经费标准化测算模型的修正由于通过传统回归方法得出的成本函数存在多重共线性,并且小学入学率 (EERt) 和初中入学率 (MERt) 系数为负值与常理不符,为了解决多重共线性问题,本文拟通过岭回归方法对教育成本函数进行再次拟合。岭回归是一种专门用于解决多元线性回归模型分析的有偏估计方法,它能够在不删减变量的基础上很好地解决变量之间存在的多重共线性问题。岭回归实际上是一种改良了的最小二乘估计,它是在自变量信息矩阵的主对角线上加入一个非负因子k,从而使得估计结果的稳定性明显提高的一种回归分析方法。目前,国内岭回归分析方法主要运用于工程管理、能源需求和光谱测量等领域,用于教育学和经济学领域的文献相对较少。参考上述研究方法和理论成果,本文运用SPSS18.0对教育成本函数进行岭回归分析,回归结果如表 3所示。
| 表 3 不同k值下的R2和β系数统计表 |
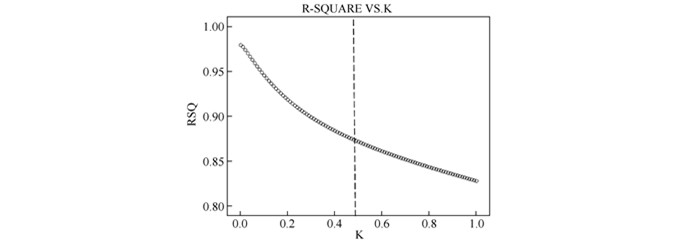
表 3中截取了部分不同k值下的R2和β系数估计值。在岭回归中,对于非负因子k值的选择尤为重要,本文基于选取k值的方差扩大因子法和何秀丽,王浩华 (2008)的均方误差函数单调法,运用SYSTAT12.0和NCSS软件进行综合判断分析后发现:当k达到0.45附近的时候,五个自变量的岭迹都开始趋于平稳,自变量中小学入学率 (EERt) 和初中入学率 (MERt) 的边际产出系数也由负值转变为正值,在图 1中做辅助参考线可以清晰看到k值超过0.45之后,决定系数一直保持平稳下降趋势,没有出现明显波动,因此该岭回归中k值确定为0.45。当k值为0.45时,函数方程的拟合优度R2为0.8788,虽然不及原方程0.9811高,但是新的教育成本函数方程中所有自变量的系数均为正数,符合教育投入产出的基本常识,岭回归正是通过舍弃少量有偏性,换来了函数方程回归系数的合理估计,新的成本函数方程如下:
|
图 1 决定系数与k值的曲线图 |
| $\begin{array}{l} E{F_t} = 0.2837{\rm{ }}PE{R_t} + 0.0229{\rm{ }}EE{R_t} + 0.0348{\rm{ }}ME{R_t} + \\ 0.2856{\rm{ }}SE{R_t} + 0.2183{\rm{ }}HE{R_t} \end{array} $ | (5) |
此外,为了使时间序列数据平滑,消除统计单位的差异性,岭回归在计算的过程中首先会对全部的变量进行标准化处理,因此输出结果中只显示出各项变量标准化后的回归系数,且不存在常数项。为了方便对教育经费标准值的实际估算,本文根据各项变量的均值和标准差对拟合出来的全国性教育成本函数方程 (5) 进行反标准化处理:
| $ {\beta _n} = {\rm{ }}\left({\frac{{{s_y}}}{{{s_x}}}} \right)*{\beta _n}^*\left({n = 1, \cdots 6} \right) $ | (6) |
| $ {\beta _0} = \bar y - {\beta _1}{{\bar x}_1} - \cdots {\beta _4}\bar x{_5} $ | (7) |
其中,βn为各项自变量的回归系数,βn*表示k值为0.45时各项自变量回归系数的估计值,β0表示常数项,sy和sx表示因变量和自变量的标准差,y和xn表示因变量和自变量的均值,结合相关数据,得出反标准化变换后的全国性教育成本函数方程最终形式:
| $ \begin{array}{l} E{F_t} = - 31866.75 + 14513.886{\rm{ }}PE{R_t} + 22594.128{\rm{ }}EE{R_t} + \\ 2503.607{\rm{ }}ME{R_t} + 9862.485{\rm{ }}SE{R_t} + 17132.834{\rm{ }}HE{R_t} \end{array} $ | (8) |
根据函数方程 (8) 可以对我国历年教育财政投入变化做出如下分析:在其他四个自变量不变的情况下,学前教育入学率每提高一个百分点 (单位统一为百分数后),需要财政性教育经费相应的增加145.139亿元;小学、初中和高中入学率每提高一个百分点,需要财政性教育经费分别增加225.941亿元、25.036亿元和98.625亿元;最后,高等教育入学率增加一个百分点则需要政府财政性教育经费多投入171.328亿元。由于高等教育中生均培养成本相对较高,中国教育财政投入又长期呈现倒金字塔型结构,岭回归中各项自变量的边际产出系数及其大小排序都基本符合我国教育财政投入的实际情况。
综合教育成本函数中学前教育入学率等自变量的边际产出系数,将前文中的全国历年教育事业发展的目标分解值代入后,即可测算出达到充足水平的全国财政性教育经费标准值。
| 表 4 全国历年财政性教育经费标准值 亿元 |
表 4中显示了各年全国财政性教育经费的标准值,在其他条件不变的情况下,标准值基本能够满足全国《教育事业发展五年规划》中各阶段入学率的增长要求,可以作为判断教育经费充足与否的参考标准。
五、 我国教育财政投入充足水平分析基于成本函数和岭回归等实证方法,前文已测算出我国财政性教育经费标准值,将其代入函数方程 (2) 中,运用Evidence-based方法则可以估算出历年教育财政充足度指数Adext的具体数值。现根据我国教育财政充足度指数的变动情况,对当前我国教育财政投入充足水平进行综合判断和分析。
(一) 能够基本满足教育事业发展需求伴随着《国家中长期教育改革和发展规划纲要 (2010-2020年)》等政策对教育财政“4%”目标的不断强化,2009年我国教育财政充足度指数首次突破1,财政性教育经费实际值与成本函数法估算出来的标准值基本持平。如表 5所示,2014年全国财政性教育经费高达26420.58亿元,比估算出来的标准值多出9678.56亿元,教育财政充足度指数攀升至1.5781③,教育财政投入4%的政策效应十分显著。目前,我国教育财政投入基本能够为公共教育发展提供较为充足的经费支持,可以满足不同时期我国《教育事业发展五年规划》中规定的各阶段教育入学率所需的经费要求。
| 表 5 我国历年教育财政充足度指数Adext统计表 亿元 |
另一方面,从测算出的数值上看,2009年以来我国教育财政充足度指数长期保持在1以上,2013年更是达到了1.5以上,然而我国教育事业在国际比较中并未展现出明显优势,上述现象集中反映了两个值得关注的问题。第一,我国及各省市历年《教育事业发展五年规划》的目标设置存在相对保守的现象,各阶段教育入学率的设置与经费投入匹配度不高。例如,青海省在其《“十二五”教育改革和发展规划》中规定2015年全省学前教育入学率为60%,而2010年青海学前教育入学率已经达到60.4%,目标设置与实际发展不相匹配。第二,我国当前各阶段教育仍处于较低层次的扩展状态,入学率的提高与教育质量提升并未实现协同发展。因此,在下一阶段的“十三五”规划中,我国可以适当调高各阶段入学率的发展目标,提高其与财政投入的匹配程度。与此同时,进一步加大对教育质量的重视力度,在未来普及高中和高等教育过程中,通过增加生均公用经费等方式,促进入学率和教育质量的共同提高。
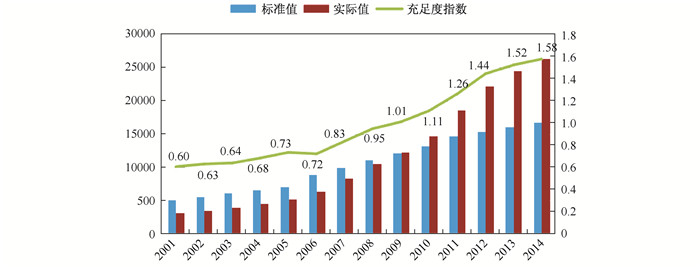
(二) 后“4%”时代的充足水平增速放缓长期以来,我国教育财政投入受教育财政投入4%行政命令的影响较大,在教育财政投入制度尚不完善的情况下,这种单一的扩展不可避免地会受到来自“教育资源稀缺性”和“行政命令红利枯竭”等方面的限制,导致财政性教育经费的增长缺乏长效性。如图 2所示,2011年,我国教育财政充足度指数为1.26,比2010年提高了近0.15个百分点,2012年增幅更是高达0.18个百分点。然而,在教育财政投入4%的目标实现之后,我国教育财政投入随即出现增速放缓的迹象,2013年教育财政充足度指数增幅迅速降至0.08个百分点,而2014年增幅仅为0.05个百分点,增幅跌至2007年以来的最小值。
|
图 2 全国历年教育财政充足度指数变化趋势图 |
受中央政府关于“2012年实现教育财政投入占GDP 4%”政策目标的影响,各级政府在教育财政投入过程中大都出现了期末突击完成任务的情况,后“4”时代的教育财政投入充足度没能保住平稳增长的趋势,我国未来教育财政投入的增长存在着较大的不确定性。因此,“十三五”教育规划的制定过程中,政府部门对教育财政投入需要通过“定标准、定责任、入预算”,确立国家标准和省级标准,确立各级政府的支出责任,继而再定经费预算数量 (王善迈,2015),从而在保障财政性教育经费充足水平的同时,努力建立和完善教育财政投入平稳增长的长效机制。
此外,随着我国县域内城乡义务教育一体化改革的推进④,在后“4”时代教育财政投入的预算过程中,还应当提高对区域间和城乡间充足水平不均衡的重视程度,在促进教育公平的同时,统筹推进教育事业一体化发展。
| 贝努瓦·米洛特. (2013). 高等教育支出与产出. 北京大学教育评论(2), 46-62. |
| 陈晓宇. (2012). 我国教育经费充足问题的回顾与展望. 教育发展研究(1), 25-29. |
| 费宇, 李晓鹏. (2006). 地方政府教育标准财政支出测算研究. 思想战线(4), 110-114. |
| 黄斌, 钟宇平. (2008). 教育财政充足的探讨及其在中国的适用性. 北京大学教育评论(1), 140-145. |
| 何秀丽, 王浩华. (2008). 岭回归中K值的探讨. 甘肃联合大学学报(6), 1-3. |
| 李政, 钟永红. (2006). 基于岭回归分析方法的中国区域经济差异影响因素分析. 统计与决策(4), 103-105. |
| 卜紫洲, 侯一麟, 王有强. (2011). 中国县级教育财政充足度考察. 清华大学教育研究(5), 35-40. |
| 孙克竞. (2011). 政府部门预算支出绩效管理改革框架构建与制度创新. 地方财政研究(8), 31-36. |
| 王善迈. (2015-6-17). "新常态"下教育经费增长的长效机制. 中国教育报, 007. |
| 杨楠. (2004). 岭回归分析在解决多重共线性问题中的独特作用. 统计与决策(3), 14-15. |
| 袁贵仁. (2013-1-25). 在2013年全国教育工作会议上的讲话. 中国教育报, 001. |
| 张文新, 李文军. (2013). 我国地方政府教育经费支出充足性探讨. 教育发展研究(23), 13-15. |
| 宗晓华. (2015). "新常态"下中国教育财政投入的可持续性与制度转型. 复旦教育论坛(6), 5-11. |
| Mukherjee Anit N. (2007). Public expenditure on education:A review of selected issues and evidence. Financing Human Development Working Paper(2), 4-22. |
| Baker B.D. (2005). The emerging shape of educational adequacy:From theoretical assumptions to empirical evidence. Journal of Education Finance(3), 259-287. |
| Glomm G., Ravikumar B. (1997). Productive government expenditures and long-run growth. Journal of Economic Dynamics and Control(21), 183-204. |
| Jay P. Greene, Greg Forster. (2002). Effects of funding incentives on special education enrollment. Civic Report(32), 4-12. |
| Le Grand Julian. (1982). The distribution of public expenditure on education. Economica(49), 63-68. |
| Liu C.L. (2008). An empircial study of the relationship between education funding investment and economic growth in China. Pioneering with Science & Technology Monthly(21), 129-132. |
| Odden A.R, Picus L.O. (2003). An evidence-based approach to school finance adequacy in Arkansas. Report prepared for the Interim Legislative Committee on Educational Adequacy |
| Picus L.O, Blair. (2004). School Finance Adequacy:The state role. Insights on Education Policy, Practice and Research(16), 1-12. |
| Rithmire M E. (2014). China's "New Regionalism": Subnational analysis in Chinese political economy. World Politics, 66(1), 165-194. DOI:10.1017/S004388711300035X |


